Algoritmi ramificați
Funcție definită pe trei intervale
`f(x)= {(x^2 , text(pentru ) x <1 text(,)),(-x , text(pentru ) 1 le x le 2 text(,)),(2*x , text(pentru ) x >2.):}`
Public Function Functie(x As Double) As Double
If (x < 1) Then
Functie = x ^ 2
Else
If (x > 2) Then
Functie = 2 * x
Else
Functie = - x
End If
End If
End Function
Algoritmi ciclici cu număr cunoscut de pași
Combinații
`C_n^k=((n),(k))=(n(n-1)(n-2)cdots(n-k+1))/(k(k-1)(k-2)cdots1)=(n(n-1)(n-2)cdots(n-k+1))/(k!)`
Programul de mai jos returnează numărul unic de combinații a n elemente luate câte k. De exemplu, numărul de mâini unice de 5 cărți luate dintr-un set de 52 de cărți este 2,598,960. Vom reveni asupra combinațiilor în capitolul vectori, unde vom lista combinațiile propriu-zise.
Public Function NumarCombinatii(n As Integer, k As Integer)
Dim i As Integer
NumarCombinatii = n
For i = 1 To k - 1
NumarCombinatii = NumarCombinatii * (n - i)
Next i
NumarCombinatii = NumarCombinatii / Factorial(k)
End Function
Private Function Factorial(n) As Double
Dim i As Integer
Factorial = 1
For i = 1 To n
Factorial = Factorial * i
Next i
End Function
Info
În exemplul de mai sus, factorialul este calculat într-o altă funcție. Funcția a fost declarată Private, astfel încât ea nu este vizibilă în afara modului în care este definită.
Algoritmi ciclici cu număr necunoscut de pași
Fibonacci
Programul de mai jos returnează termenul din șirul lui Fibonacci, mai mic decât n. Șirul lui Fibonacci, 0, 1, 1, 2, 3, 5, 8, 13, 21, … este definit prin relația de recurență:
`F_i=F_(i-2)+F_(i-1)`, unde
`F_1=0,F_2=1`
Function Fibonacci(ByVal n As Integer)
' Calculul termenului din sirul lui Fibonacci mai mic decat n
Dim Fibo1 As Integer, Fibo2 As Integer, Fibo As Integer
Fibo1 = 0
Fibo2 = 1
Fibo = Fibo1 + Fibo2
Do While Fibo < n
Fibo1 = Fibo2
Fibo2 = Fibo
Fibo = Fibo1 + Fibo2
Loop
Fibonacci = Fibo2
End Function
Calculul constantei e
Pentru calculul constantei `e` putem folosi dezvoltarea în serie:
`e=1+1/(1!)+1/(2!)+1/(3!)+cdots+1/(n!)`
Function E()
Const Precizie As Double = 0.001
Dim i As Long, Factorial As Double, Termen As Double
E = 1
i = 1
Factorial = 1
Termen = 1
Do While (Termen > Precizie)
E = E + Termen
i = i + 1
Factorial = Factorial * i
Termen = 1 / Factorial
Loop
End Function
Cosinusul unui unghi
Pentru calculul cosinusului unui unghi `x` (în radiani) putem folosi dezvoltarea în serie:
`cos(x)=1-x^2/(2!)+x^4/(4!)-x^6/(6!)+cdots+(-1)^nx^(2n)/(2n!)`
Funcția vb este dată mai jos:
Function Cosinus(x As Double)
Const Precizie As Double = 0.001
Dim Factorial As Double
Dim Contor As Double
Dim Cos As Double
Dim Curent As Double
Cos = 1
Curent = 1
Contor = 2
Factorial = 1
Do While Abs(Curent / Factorial) > Precizie
Curent = -Curent
Curent = Curent * x ^ 2
Factorial = Factorial * (Contor - 1) * Contor
Cos = Cos + Curent / Factorial
Contor = Contor + 2
Loop
Cosinus = Cos
End Function
Funcții
Calculul integralei unei funcții cu metoda lui Simpson (1/3)
`int_a^b f(x) dx~~h/3[f(x_0)+2sum_(i=1)^(n//2-1)f(x_(2i))+4sum_(i=1)^(n//2)f(x_(2i-1))+f(x_n)]`
cu `x_i=a+ih`, unde `i=0,1,cdots,n-1,n`, pasul `h=(b-a)/n`, in particular `x_0=a,x_n=b`
`int_a^b f(x) dx~~h/3[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+cdots+4f(x_(n-1))+f(x_n)]`
Option Explicit
Function SimpsonIntegral(Functia As String, Xstart As Double, Xend As Double, Intervale As Long) As Variant
Dim i As Long, Pas As Double, Integrala As Double
' Facem numarul de intervale par
Intervale = 2 * Intervale
Pas = (Xend - Xstart) / Intervale
' Calculam valoarea functiei in a
Integrala = ValoareaFunctiei(Functia, Xstart)
' Adaugam termenii impari
For i = 1 To Intervale - 1 Step 2
Integrala = Integrala + 4 * ValoareaFunctiei(Functia, Xstart + i * Pas)
Next i
' Adaugam termenii pari
For i = 2 To Intervale - 2 Step 2
Integrala = Integrala + 2 * ValoareaFunctiei(Functia, Xstart + i * Pas)
Next i
' Adaugam valoarea functiei in b
Integrala = Integrala + ValoareaFunctiei(Functia, Xend)
' Rezultatul final se imparte la 3
SimpsonIntegral = Integrala * Pas / 3
End Function
Private Function ValoareaFunctiei(ExpresiaFunctiei As String, Valoare As Double) As Double
' Evalueaza functia definita in x pentru un numar
' Examplu: ValoareaFunctiei("5 * xi + 3", 2) returneaza 5 * 2 + 3 = 13
Dim Expresie As String
Expresie = Replace(ExpresiaFunctiei, "xi", Valoare)
ValoareaFunctiei = Evaluate(Expresie)
End Function
`int_0^5 x^4 dx=x^5/5|_0^5=625`
`int_0^pi sin(x) dx=-cos(x)|_0^pi=2`
`int_0^pi sin(x)/x dx~~1.85194`
Descărcați fișierul Excel: Simpson.xls
Vectori
Aria unui poligon simplu
Pentru un poligon orientat trigonometric compus din segmente de dreapta definite de vârfurile `(x_i,y_i), i=0, n-1`, cu ultimul vârf `(x_n,y_n)` identic cu primul (poligon închis), aria poate fi determinată cu formula:
`A=1/2sum_(i=0)^(n-1)(x_iy_(i+1)-x_(i+1)y_i)`
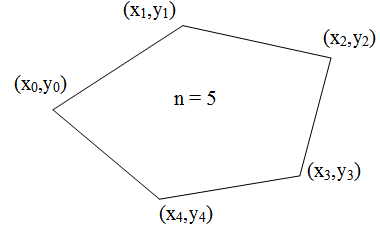
Semnul ariei obținută cu relația de mai sus poate indica orientarea poligonului. Dacă semnul este pozitiv, poligonul este definit trigonometric, dacă este negativ, varfurile sunt ordonate în sensul acelor de ceasornic.
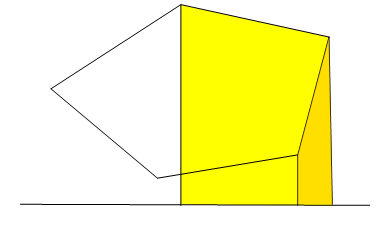
Formula este obținută din însumarea ariilor trapezelor care sunt definite de segmentele poligonului și proiecția vârfurilor pe axa orizontală. Unele vor avea arii pozitive, pe când altele vor fi negative, scăzându-se din suma totală a ariei.
Function AriaPoligonTrapez(CoordX As Range, CoordY As Range)
Dim X() As Double, Y() As Double
Dim i As Integer, j As Integer, n As Integer
Dim Arie As Double
n = CoordX.Rows.Count
ReDim X(1 To n)
ReDim Y(1 To n)
For i = 1 To n
X(i) = CoordX(i)
Y(i) = CoordY(i)
Next i
For i = 1 To n - 1
Arie = Arie + (X(i + 1) - X(i)) * (Y(i + 1) + Y(i)) / 2
Next i
AriaPoligonTrapez = Arie
End Function
Function AriaPoligonTopo(CoordX As Range, CoordY As Range)
Dim X() As Double, Y() As Double
Dim i As Integer, j As Integer, n As Integer
Dim Arie As Double
n = CoordX.Rows.Count
ReDim X(1 To n)
ReDim Y(1 To n)
For i = 1 To n
X(i) = CoordX(i)
Y(i) = CoordY(i)
Next i
For i = 1 To n - 1
Arie = Arie + X(i) * Y(i + 1) - X(i + 1) * Y(i)
Next i
Arie = Arie + X(n) * Y(1) - X(1) * Y(n)
Arie = Arie / 2
AriaPoligonTopo = Arie
End Function
Function AriaPoligonTopoV2(CoordX As Range, CoordY As Range)
Dim X() As Double, Y() As Double
Dim i As Integer, j As Integer, n As Integer
Dim Arie As Double
n = CoordX.Rows.Count
ReDim X(1 To n)
ReDim Y(1 To n)
For i = 1 To n
X(i) = CoordX(i)
Y(i) = CoordY(i)
Next i
For i = 1 To n
j = i Mod n + 1
Arie = Arie + X(i) * Y(j) - X(j) * Y(i)
Next i
Arie = Arie / 2
AriaPoligonTopoV2 = Arie
End Function
Centrul de greutate al unui poligon simplu
`c_x=1/(6A)sum_(i=0)^(n-1)(x_i+x_(i+1))(x_iy_(i+1)-x_(i+1)y_i)`
`c_y=1/(6A)sum_(i=0)^(n-1)(y_i+y_(i+1))(x_iy_(i+1)-x_(i+1)y_i)`
Function CentruPoligon(CoordX As Range, CoordY As Range)
Dim X() As Double, Y() As Double
Dim Cx As Double, Cy As Double, Aria As Double
Dim i As Integer, n As Integer
n = CoordX.Rows.Count
ReDim X(1 To n)
ReDim Y(1 To n)
For i = 1 To n
X(i) = CoordX(i)
Y(i) = CoordY(i)
Next i
For i = 1 To n - 1
Aria = Aria + (X(i) * Y(i + 1) - X(i + 1) * Y(i))
Cx = Cx + (X(i) + X(i + 1)) * (X(i) * Y(i + 1) - X(i + 1) * Y(i))
Cy = Cy + (Y(i) + Y(i + 1)) * (X(i) * Y(i + 1) - X(i + 1) * Y(i))
Next i
Aria = Aria + (X(n) * Y(1) - X(1) * Y(n))
Cx = Cx + (X(n) + X(1)) * (X(n) * Y(1) - X(1) * Y(n))
Cy = Cy + (Y(n) + Y(1)) * (X(n) * Y(1) - X(1) * Y(n))
Aria = Aria / 2
Cx = Cx / (6 * Aria)
Cy = Cy / 6 / Aria
Dim Results(1 To 3) As Double
Results(1) = Aria
Results(2) = Cx
Results(3) = Cy
CentruPoligon = WorksheetFunction.Transpose(Results)
End Function
Descărcați fișierul Excel: Poligoane.xls
Combinații II
Următoarea subrutină tipărește în fereastra Immediate combinațiile elementelor luate câte k. Subrutina este prepopulată cu o serie de 5 elemente, de la 1 la 5, și va tipări combinații de 5 luate câte 3. Nu uitați de directiva Option Base 1, altfel vectorul elemente va avea primul indice 0 și subrutina va eșua.
Option Base 1
Public Sub PrintCombinatii()
Dim elemente, n As Integer, k As Integer
Dim idx() As Integer
elemente = Array(1, 2, 3, 4, 5)
n = UBound(elemente) - LBound(elemente) + 1
k = 3
ReDim idx(1 To k)
For i = 1 To k
idx(i) = i
Next i
Do
' Afiseaza combinatia curenta
For j = 1 To k
Debug.Print elemente(idx(j));
Next j
Debug.Print
' Locate last non-max index
i = k
While (idx(i) = n - k + i)
i = i - 1
If i = 0 Then
' Toti indicii au ajuns la max, deci am termint
Exit Sub
End If
Wend
'Incrementam si populam urmatorii indici
idx(i) = idx(i) + 1
For j = i + 1 To k
idx(j) = idx(i) + j - i
Next j
Loop
End Sub
Matrici
Rezolvarea sistemelor de ecuații lineare prin metoda lui Gauss
`[(a_(11), a_(12), cdots , a_(1n)),(a_(21), a_(22), cdots , a_(2n)),(vdots, vdots, ddots, vdots),(a_(n1), a_(n2), cdots , a_(n n))] [(x_1),(x_2),(vdots),(x_n)]=[(b_1),(b_2),(vdots),(b_n)]`
Function GaussLinear(MatA As Range, MatB As Range)
Dim A, B() As Double, X() As Double
Dim n As Integer, i As Integer, j As Integer, k As Integer
Dim Factor As Double, Suma As Double
n = MatA.Rows.Count
ReDim B(1 To n)
ReDim X(1 To n)
' Citire matricea A
A = MatA
' Citire vector B
For i = 1 To n
B(i) = MatB(i)
Next i
' Eliminare inainte (triangularizarea matricii A)
For i = 1 To n - 1
For j = i + 1 To n
Factor = A(j, i) / A(i, i)
For k = i + 1 To n
A(j, k) = A(j, k) - Factor * A(i, k)
Next k
B(j) = B(j) - Factor * B(i)
Next j
Next i
' Substitutie inversa
X(n) = B(n) / A(n, n)
For i = n - 1 To 1 Step -1
Suma = 0
For j = n To i + 1 Step -1
Suma = Suma + A(i, j) * X(j)
Next j
X(i) = (B(i) - Suma) / A(i, j)
Next i
' Returnarea vectorului X
GaussLinear = WorksheetFunction.Transpose(X)
End Function
Descărcați fișierul Excel: Gauss.xls